Wyznaczanie
prędkości głosu za pomocą interferometru Quinckego . (210)
OPIS TEORETYCZNY
To ćwiczenie, podobnie jak ćwiczenie z rurą Quinckego
dotyczy badania rozchodzenia się fal dźwiękowych w powietrzu.
CEL ĆWICZENIA
Celem ćwiczenia jest wyznaczenie prędkości dźwięku w powietrzu w temperaturze
otoczenia i w warunkach normalnych.
METODA POMIAROWA
Interferometr Quinckego jest przyrządem skontruowanym w ten sposób, aby
doprowadzić do interferencji dwóch wiązek akustycznych.
Zasada działania jest następująca:
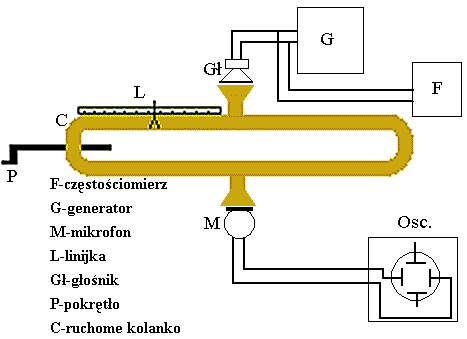
Drgania elektryczne uzyskane z generatora drgań akustycznych G
(drgań, o częstotliwościach odpowiadających częstotliwościom zakresu fal słyszlnych przez ucho ludzkie,
a więc od ok. 20Hz do ok. 20kHz)
kierowane są do głośnika Gł, skąd, jako fala dźwiękowa, kierowane są
do rurki metalowej, służącej za falowód.
Rurka ta rozgałęzia się, dzięki czemu fala dzieli się na dwie wiązki, które
następnie spotykają się ponownie w miejscu, gdzie rurki te łączą się ponownie.
W miejscu tym umieszczony jest mikrofon M, zamieniający falę dźwiękową na drgania
elektryczne, których przebieg można obserwować na ekranie oscyloskopu Osc.
Spotykające się fale są spójne, gdyż pochodzą z jednego źródła,
a więc mogą ze sobą interferować . Aby uzyskać
wzmocnienie (osłabienie)interferencyjne, należy doprowadzić do spotkania tych fal
w zgodnej (przeciwnej) fazie,
Uzyskujemy to zmieniając długość odcinka drogi przebytego przez jedną z fal, dzięki ruchomemu,
wygiętemu odcinkowi rurki RR (jak w puzonie). Gdy przebyte przez te fale
odcinki drogi będą różnić się o wielokrotność długości fali, fale spotkają się w zgodnej fazie.
Gdy przebyte przez te fale
odcinki drogi będą różnić się o nieparzystą wielokrotność
połowy długości fali, fale spotkają się w przeciwnej fazie.
My nie mierzymy jednak długośći dróg przebytych przez
poszczególne fale, gdyż
konstrukcja interferometru pozwala nam wyznaczyć odcinek l
będący połową różnicy dróg między dwoma kolejnymi wzmocnieniami (osłabieniami).
Widać to na rysunku:
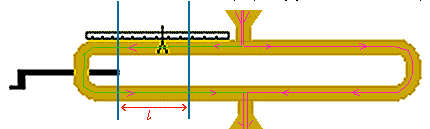 Dzięki umiejscowieniu mikrofonu w miejscu spotkania fal wynik nakładania
się fal można obserwować na ekranie oscyloskopu, a położenie rurki w momencie
odczytać na przymiarze milimetrowym L.
Niezależnie od tego, czy wyznaczamy położenie dwóch sąsiednich minimów (łatwiej
zaobserwować) czy maksimów, odległość między nimi (zmierzona linijką L) spełnia zależność :
Dzięki umiejscowieniu mikrofonu w miejscu spotkania fal wynik nakładania
się fal można obserwować na ekranie oscyloskopu, a położenie rurki w momencie
odczytać na przymiarze milimetrowym L.
Niezależnie od tego, czy wyznaczamy położenie dwóch sąsiednich minimów (łatwiej
zaobserwować) czy maksimów, odległość między nimi (zmierzona linijką L) spełnia zależność :
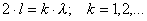
(różnica dróg=długości fali)
Można więc (biorąc pod uwagę dwa sąsiednie minima - k=1)łatwo obliczyć prędkość
dźwięku w temperaturze otoczenia:
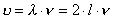
i w warunkach normalnych:
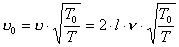
Ten ostatni wzór wynika z wyprowadzenia
PRZEBIEG POMIARÓW
- Włączyć generator, oscyloskop i częstościomierz
- Przy ustalonej częstotliwości drgań generator akustycznego (np. 1500 Hz
przesuwać kolanko interferometru C przy pomocy śruby P;
odczytując na skali L wartości l1 i l2 odpowiadające dwu
kolejnym osłabieniom dźwięku (minimalna amplituda na ekranie
oscyloskopu); pomiary wykonać co najmniej trzykrotnie.
- Pomiary z punktu (2) wykonać dla kilku innych częstotliwości
(mniejszych i większych od poprzedniej), uzgodnionych z prowadzącym zajęcia.
- Zanotować temperaturę otoczenia, dokładność termometru
(T, oraz dokładność częstościomierza
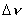
- Przeprowadzić obliczenia, wyniki przedstawić w postaci:
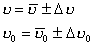
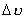 i
i 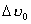 to całkowite
niepewności pomiaru prędkości dźwięku. Sposób jej obliczenia
podałem na końcu tej strony)
to całkowite
niepewności pomiaru prędkości dźwięku. Sposób jej obliczenia
podałem na końcu tej strony)
- Wyniki pomiarów i obliczeń zapisać w tabeli.
Tabela:
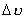 to całkowita niepewność pomiaru, uwzględniająca zarówno niepewności przypadkowe,
jak i systematyczne. Należy obliczyć ją ze wzoru:
to całkowita niepewność pomiaru, uwzględniająca zarówno niepewności przypadkowe,
jak i systematyczne. Należy obliczyć ją ze wzoru:
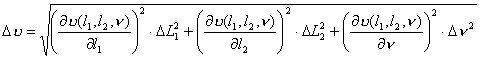
Przed podstawieniem do powyższego wzoru należy najpierw obliczyć
 L1 i
L1 i  L2,
które oznaczają tu całkowite odchylenia standardowe, oraz pochodne z wzoru:
L2,
które oznaczają tu całkowite odchylenia standardowe, oraz pochodne z wzoru:
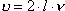
Niepewności  L1 i
L1 i  L2
obliczamy ze wzorów:
L2
obliczamy ze wzorów:
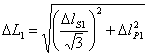
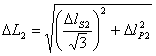
są one związane :
- z niepewnościami systematycznymi
(będę je oznaczać jako
 lS1 i
lS1 i  lS2); przy obecnie funkcjonującym zestawie doświadczalnym
wydaje się rozsądnym przyjęcie tych wielkości na 0,5cm
lS2); przy obecnie funkcjonującym zestawie doświadczalnym
wydaje się rozsądnym przyjęcie tych wielkości na 0,5cm
- z niepewnościami przypadkowymi (
 lP1
i
lP1
i  lP2)
lP2)
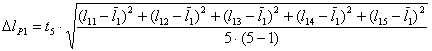
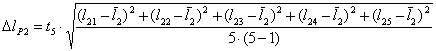
we wzorach tych:
- l11,...,l15 to kolejne wyniki pomiarów długości l1,
- l21,...,l25 to kolejne wyniki pomiarów długości l2
i są pobierane z powyższej tabeli (która sugeruje wykonanie po 5 pomiarów każdej odległości l).
Współczynnik Studenta
t5 wybieramy dla zadanego poziomu ufności z tabeli współczynników Studenta-Fischera
(np. dla poziomu ufności 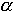 =0,3174 wynosi on t5=1,1414 )
=0,3174 wynosi on t5=1,1414 )
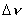 jest związane wyłącznie z niepewnością
systematyczną (odczytu częstotliwości dokonujemy tylko raz) i określona jest przez dokładność
użytego częstościomierza.
jest związane wyłącznie z niepewnością
systematyczną (odczytu częstotliwości dokonujemy tylko raz) i określona jest przez dokładność
użytego częstościomierza.
Potrzebne do wzoru pochodne wynoszą :
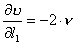
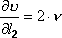
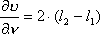
Teraz trzeba już tylko podstawić wartości liczbowe do pierwszego z podanych wzorów.
Takie same obliczenia należy przeprowadzić dla dwóch pozostałych częstotliwości.
Ponieważ nie mamy żadnych informacji na temat wielkości
dyspersji fal dźwiękowych w danych warunkach,
wyznaczamy trzy różne wartości prędkości dźwięku.
Nie uwzględniając dyspersji można obliczyć średnią wartość prędkości dźwięku i
jej niepewność jako odchylenie standardowe wartości średniej.
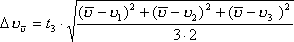
Pozostaje jeszcze obliczyć niepewność pomiaru 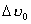 .
.
Korzystając z zależności
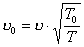
otrzymamy na tę niepewność następującą zależność:
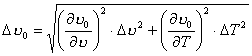
We wzore tym 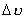 mamy już wyznaczone,
mamy już wyznaczone,
 T określa niepewność systematyczną pomiaru temperatury
(wynika z dokładności użytego termometru)
T określa niepewność systematyczną pomiaru temperatury
(wynika z dokładności użytego termometru)
Także tu, pomijając dyspersję, należy obliczyć wartość średnią z
trzech wartosci  0 i
jej odchylenie standardowe tak jak poprzednio
0 i
jej odchylenie standardowe tak jak poprzednio



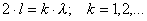
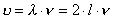
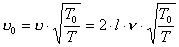
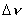
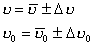
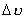 i
i 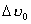 to całkowite
niepewności pomiaru prędkości dźwięku. Sposób jej obliczenia
podałem na końcu tej strony)
to całkowite
niepewności pomiaru prędkości dźwięku. Sposób jej obliczenia
podałem na końcu tej strony)
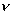
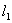
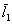
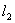
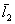

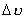
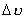 to całkowita niepewność pomiaru, uwzględniająca zarówno niepewności przypadkowe,
jak i systematyczne. Należy obliczyć ją ze wzoru:
to całkowita niepewność pomiaru, uwzględniająca zarówno niepewności przypadkowe,
jak i systematyczne. Należy obliczyć ją ze wzoru: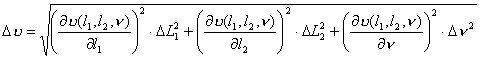
 L1 i
L1 i  L2,
które oznaczają tu całkowite odchylenia standardowe, oraz pochodne z wzoru:
L2,
które oznaczają tu całkowite odchylenia standardowe, oraz pochodne z wzoru: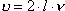
 L1 i
L1 i  L2
obliczamy ze wzorów:
L2
obliczamy ze wzorów: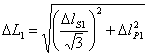
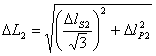
 lS1 i
lS1 i  lS2); przy obecnie funkcjonującym zestawie doświadczalnym
wydaje się rozsądnym przyjęcie tych wielkości na 0,5cm
lS2); przy obecnie funkcjonującym zestawie doświadczalnym
wydaje się rozsądnym przyjęcie tych wielkości na 0,5cm
 lP1
i
lP1
i  lP2)
lP2)
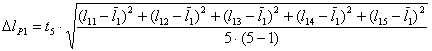
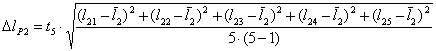
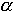 =0,3174 wynosi on t5=1,1414 )
=0,3174 wynosi on t5=1,1414 )
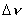 jest związane wyłącznie z niepewnością
systematyczną (odczytu częstotliwości dokonujemy tylko raz) i określona jest przez dokładność
użytego częstościomierza.
jest związane wyłącznie z niepewnością
systematyczną (odczytu częstotliwości dokonujemy tylko raz) i określona jest przez dokładność
użytego częstościomierza.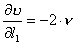
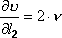
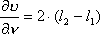
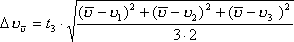
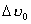 .
.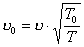
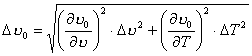
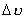 mamy już wyznaczone,
mamy już wyznaczone,
 T określa niepewność systematyczną pomiaru temperatury
(wynika z dokładności użytego termometru)
T określa niepewność systematyczną pomiaru temperatury
(wynika z dokładności użytego termometru) 0 i
jej odchylenie standardowe tak jak poprzednio
0 i
jej odchylenie standardowe tak jak poprzednio