 Wyznaczanie współczynnika rozszerzalności liniowej metalu .
Wyznaczanie współczynnika rozszerzalności liniowej metalu .
(112)
OPIS TEORETYCZNY
Większość ciał zarówno stałych, ciekłych jak i gazowych wraz ze wzrostem temperatury
i przy stałym ciśnieniu (naprężeniu) zwiększa swoje rozmiary (wyjątkiem jest np. woda w zakresie temperatur 0oC do 4 oC)
Na tej stronie zajmę się jednak głównie rozszerzalnością cieplną ciał stałych nie związaną ze zmianą stanu skupienia.
Wyobraźmy sobie model ciała krystalicznego, w którym atomy ułożone są regularnie w przestrzeni dzięki wzajemnym
oddziaływaniom pochodzenia elektrycznego. Siły oddziaływania między atomami są zbliżone do sił występujących między
niewielkimi kuleczkami połączonymi sprężynkami, jak na rysunku poniżej:
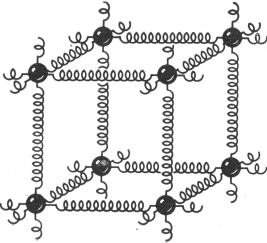
Przy zbliżaniu kulki odpychają się, przy oddalaniu przyciągają się.
Atomy drgają. Gdy temperatura rośnie, rośnie również energia kinetyczna tych atomów, a więc i amplituda tych drgań.
Analogia nie jest jednak pełna.
W rzeczywistości oddziaływanie między cząsteczkami jest nieco bardziej skomplikowane.
Siły jakie działają pomiędzy cząsteczkami w sieci krystalicznej nie są siłami sprężystymi (nie są proporcjonalne do wychylenia z położenia równowagi x)
i zależą od przesunięcia x względem położenia równowagi zgodnie z zależnością:
Fx = -Kx + bx2, gdzie K jest współczynnikiem siły quasi-sprężystej, a b współczynnikiem anharmoniczności drgań.
Wyrażenie bx2 opisuje odchylenie drgań od harmoniczności.
Obrazowo można przedstawić to w oparciu o wykres przedstawiający oddziaływanie dwóch sąsiednich atomów.
Jeżeli początek układu współrzędnych związany jest z jednym z rozpatrywanych atomów,
to siła działająca na drugi przedstawia się tak, jak na poniższym wykresie:
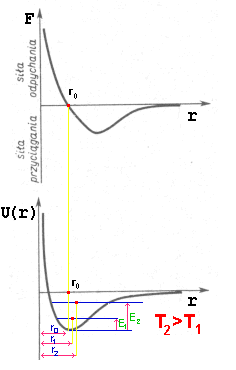
Z wykresu widać, że dla pewnej odległości
r=r0 siła staje się równa zeru - wzajemne oddziaływania przyciągające i odpychające znoszą się.
Odpowiada to stanowi równowagi trwałej (minimalna energia potencjalna ).
Gdy atomy zbliżają się, decydującą rolę odgrywają siły odpychające i energia potencjalna U szybko rośnie.
Gdy atomy oddalają się, decydującą rolę odgrywają, nieco słabsze, siły przyciągające
Pamiętając o tym, że F= -dU/dr, możemy zaobserwować, jak zmienia się siła, w zależności od energii potencjalnej
oddziaływania między atomami.
Jak widać wykres energii potencjalnej jest asymetryczny. Z tej asymetryczności wynika, że gdy rośnie energia drgań
(od E1 do E2) czyli, gdy rośnie temperatura (od T1 do T2),
rośnie również średnia odległość między atomami (od r1 do r2).
- r0, r1 i r2 to średnia odległość między atomami w coraz wyższych temperaturach.
Warto zwrócić uwagę, że gdyby krzywa energii potencjalnej była symetryczna
i wychylenie atomów w prawo i w lewo byłoby takie samo
niezależnie od wielkości amplitudy drgań, to średnia odległość
między atomami byłaby stała (równa r0), niezależnie od temperatury.
Nie byłoby więc rozszerzalności termicznej, która, jak z tego wynika, jest właśnie konsekwencją tej niesymetryczności.
Można wykazać, że średnie przemieszczenie wyraża zależność:
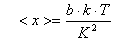
Widać więc, że ze wzrostem temperatury rośnie średnia odległość między cząsteczkami
sieci krystalicznej i ciało rozszerza się.
Współczynnik rozszerzalności liniowej 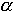 jest związany ze współczynnikiem
anharmoniczności wzorem:
jest związany ze współczynnikiem
anharmoniczności wzorem:
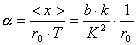
Niektóre ciała krystaliczne mogą w pewnych zakresach temperatur zmniejszać swe rozmiary wraz ze wzrostem temperatury. Jest tak, gdy drgania
poprzeczne cząsteczek są większe niż drgania podłużne, co prowadzi do ujemnego współczynnika rozszerzalności
w pewnych kierunkach. Tych przypadków nie będę tu rozpatrywał.
Zajmę się teraz zjawiskiem tzw rozszerzalności liniowej ciał stałych, czyli zmianą rozmiarów ciała w jednym, wybranym kierunku.
Wyobraźmy sobie pręt, który w pewnej temperaturze to ma długość lo, a w temperaturze t
ma długość l, jak na poniższym rysunku:
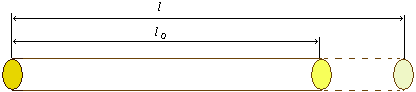
Doświadczenie uczy, że gdy różnica temperatur jest nie większa niż kilkadziesiąt stopni, przyrost długości
 l= l- lo
jest proporcjonalny do przyrostu temperatur
l= l- lo
jest proporcjonalny do przyrostu temperatur  t= t- to
t= t- to
Współczynnik proporcjonalności oznacza się zazwyczaj literą 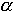 i nazywa współczynnikem
rozszerzalności liniowej.
i nazywa współczynnikem
rozszerzalności liniowej.
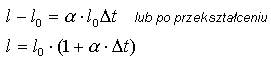
Jest to średnia wartość tego współczynnika w danym zakresie temperatur.
Współczynnik 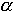 wyraża się w K-1.
Średnie wartości jakie przyjmuje ten współczynnik, to na przykład:
wyraża się w K-1.
Średnie wartości jakie przyjmuje ten współczynnik, to na przykład:
- glin - 0,0000240 K-1
- miedź - 0,0000170 K-1
- stal - 0,0000110 K-1
- porcelana - 0,0000035 K-1
- szkło - 0,0000030 K-1
Podany wyżej wzór jest jednocześnie "receptą" na wyznaczenie tego współczynnika. Wystarczy przekształcić go do postaci:
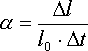
W miarę zmiany temperatury zmieniają się wszystkie wymiary ciała, zmienia się więc objętość ciała.
Dlatego też wprowadza się również pojęcie współczynnika rozszerzalności objętościowej ciała,
który oznacza się zazwyczaj literą 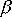 .
.
Jeżeli wszystkie trzy wymiary zmieniają się jednakowo (mają ten sam współczynnik rozszerzalności liniowej)
to objętość V ciała w temperaturze t można wyrazić przez jego objętość Vo w temperaturze
to w następujący sposób:
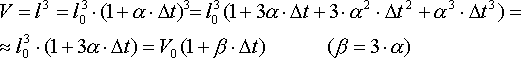
Wykorzystałem tu fakt, że 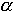 2 oraz
2 oraz
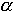 3 są bardzo małe (patrz przykłady typowych wartości współczynników
3 są bardzo małe (patrz przykłady typowych wartości współczynników 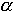 )
i jednomiany, w których one występują można pominąć jako niezmiernie małe.
)
i jednomiany, w których one występują można pominąć jako niezmiernie małe.
Wówczas współczynnik rozszerzalności objętościowej ciała 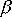 jest trzykrotnie większy
od współczynnika rozszerzalności liniowej
jest trzykrotnie większy
od współczynnika rozszerzalności liniowej 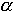 , czyli
, czyli
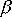 = 3
= 3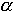 .
.
Wraz z temperaturą rośnie objętość (i maleje gęstość) nie tylko większości ciał stałych, ale i cieczy.
Wyjątek stanowi woda, która zachowuje się nietypowo w zakresie temperatur od 0oC do 4oC,
jak przedstawia to poniższy wykres:
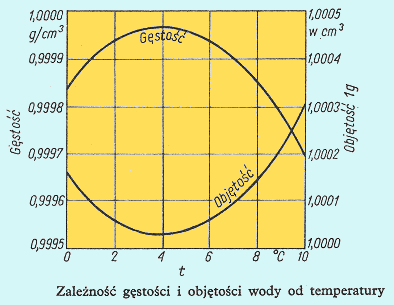
Jak wynika z wykresu, w tym przypadku nie można mówić o liniowości rozszerzalności objętościowej.
CEL ĆWICZENIA
Celem ćwiczeniem jest wyznaczenie średniego współczynnika rozszerzalności liniowej kilku wybranych
metali.
METODA POMIAROWA
Wspólczynnik rozszerzalności liniowej wyznaczamyw oparciu o zależność
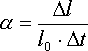
Oznacza to, że należy wyznaczyć:
- długość początkową lo,
- różnicę temperatur
 t
t
- związene z nią wydłużenie badanego ciała
 l
l
Do doświadczenia użyjemy cienkich (kilka mm) prętów metalowych o długości ok. 40cm.
Ponieważ mierzone wydłużenie jest niewielkie, do pomiaru zmiany długości wykorzystamy przyrząd zwany dylatometrem,
który posiada bardzo precyzyjny miernik pozwalający mierzyć zmiany długości pręta z dokładnością 0,01mm (10-5m)
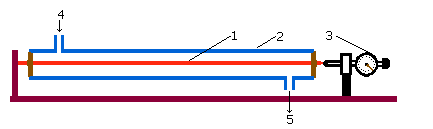
- 1-Badany pręt,
- 2-Płaszcz szklany,
- 3-Miernik wydłużenia,
- 4-Wlot pary,
- 5-Wylot pary i skroplonej wody.
Za początkową temperaturę pręta (to) będziemy przyjmować temperaturę otoczenia,
gdyż przed pomiarem pręty od dłuższego czasu przebywają w pomieszczeniu i można przyjąć, że są w równowadze termodynamicznej z otaczającym je powietrzem).
Końcową temperaturą będzie za każdym razem temperatura wrzenia wody.
Określimy ją z tablic,
na podstawie pomiaru ciśnienia
atmosferycznego.
(Patrz opis do ćwiczenia Wyznaczanie temperatury wrzenia wody w zależności od ciśnienia)
Aby pręt uzyskał dokładnie temperaturę wrzącej wody, otoczony jest szklanym płaszczem, do wnętrza którego wpuszczana jest
przez dłuższy czas para doprowadzona z kolby z gotującą się wodą.
Obserwując wskazówkę wskaźnika wydłużenia, należy zaobserwować jej położenie początkowe (w temperaturze to)
i położenie końcowe- gdy wskazówka w ciągu 2-3 minut nie przesunie się dalej, mimo doprowadzania gorącej pary.
OPRACOWANIE WYNIKÓW POMIARÓW
Opracowanie wyników opisane jest w instrukcji do ćwiczenia
Jako niepewność pomiaru różnicy temperatur u( T) przyjąć należy dokładność termometru, z którego odczytano temperaturę początkową, gdyż temperatura końcowa odczytana z tabel jest wzięta z bardzo dużą dokładnością
T) przyjąć należy dokładność termometru, z którego odczytano temperaturę początkową, gdyż temperatura końcowa odczytana z tabel jest wzięta z bardzo dużą dokładnością




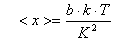
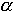 jest związany ze współczynnikiem
anharmoniczności wzorem:
jest związany ze współczynnikiem
anharmoniczności wzorem: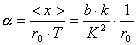

 l= l- lo
jest proporcjonalny do przyrostu temperatur
l= l- lo
jest proporcjonalny do przyrostu temperatur  t= t- to
t= t- to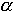 i nazywa współczynnikem
rozszerzalności liniowej.
i nazywa współczynnikem
rozszerzalności liniowej.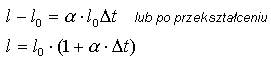
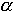 wyraża się w K-1.
Średnie wartości jakie przyjmuje ten współczynnik, to na przykład:
wyraża się w K-1.
Średnie wartości jakie przyjmuje ten współczynnik, to na przykład: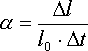
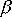 .
.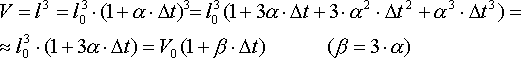
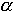 2 oraz
2 oraz
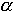 3 są bardzo małe (patrz przykłady typowych wartości współczynników
3 są bardzo małe (patrz przykłady typowych wartości współczynników 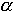 )
i jednomiany, w których one występują można pominąć jako niezmiernie małe.
)
i jednomiany, w których one występują można pominąć jako niezmiernie małe.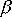 jest trzykrotnie większy
od współczynnika rozszerzalności liniowej
jest trzykrotnie większy
od współczynnika rozszerzalności liniowej 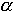 , czyli
, czyli 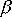 = 3
= 3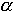 .
.
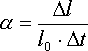
 t
t  l
l
 T) przyjąć należy dokładność termometru, z którego odczytano temperaturę początkową, gdyż temperatura końcowa odczytana z tabel jest wzięta z bardzo dużą dokładnością
T) przyjąć należy dokładność termometru, z którego odczytano temperaturę początkową, gdyż temperatura końcowa odczytana z tabel jest wzięta z bardzo dużą dokładnością