Wyznaczanie współczynnika lepkości cieczy za pomocą wiskozymetru Hoepplera .
(115)
 OPIS TEORETYCZNY
OPIS TEORETYCZNY
W wielu przypadkach ciecze rzeczywiste zachowują się w przyblizeniu jak ciecz doskonała,
tzn. nielepka i nieściśliwa.
Dla cieczy nieściśliwej słuszne jest prawo ciągłości przepływu.
Wynika z niego, że rurze ciecz osiąga największą prędkość w miejscach o małej powierzchni przekroju.
Z drugiej strony prędkość cieczy w rurze zależy od ciśnień: statycznego i hydrodynamicznego, o czym
mówi równanie Bernoulliego.
Oba te prawa nie uwzględniają różnicy prędkości cząsteczek cieczy znajdujących się w różnej odległości od ścianek rury, gdyż
nie uwzględniają tarcia między cząsteczkami cieczy, tzw. tarcia wewnętrznego.
Wskutek tarcia wystepującego między cząsteczkami cieczy, poruszająca się cząsteczka pociąga za sobą sąsiadujące cząsteczki tym silniej,
im większa jest siła lepkości. Te cząsteczki pociągają następne itd... Każda następna warstwa porusza się jednak nieco wolniej,
tym wolniej, im mniejsza lepkość cieczy. Prędkość spada do zera dla cząstek przy ściankach, które są jakby "przyklejone",
a więc nieruchome.Tak więc maksymalną prędkość mają cząsteczki na osi rury, jak pokazuje to rysunek:
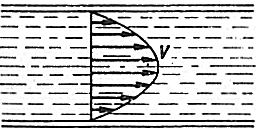
Taka sytuacja ma miejsce przy małych prędkościach cieczy przez gładką rurę. Mówimy,
że przepływ jest laminarny, czyli warstwowy. Kolejne warstwy cieczy płyną nie zakłócając się wzajemnie.
Przy dużych prędkościach w cieczy popjawiają się zawirowania i ruch z laminarnego
zmienia się w turbulentny. Rozkład prędkości jest wtedy nieco inny:
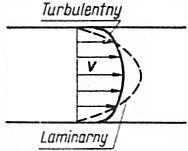
Do określenia lepkości cieczy posłużymy się takim modelem:
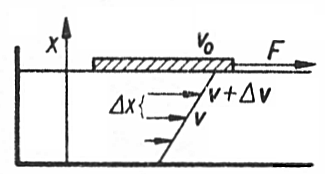
Płaską deseczkę leżąca na powierzchni cieczy w szerokim, płytkim naczyniu, ciągniemy siłą F,
nadając jej stałą prędkość v0.
Warstwa cieczy przylegająca do deseczki ma prędkość taką samą jak deseczka, a kolejne, leżące coraz głębiej warstwy,
mają prędkości coraz mniejsze. Warstwa cieczy przylegająca do dna jest nieruchoma. Zatem im płytsze naczynie, tym szybciej
maleje wraz z głębokością prędkość cieczy.
Z doświadczenia wynika, że wielkość tych zmian powiązna jest z działającą siłą zależnością:
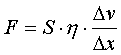
lub ogólniej
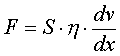
S to powierzchnia deseczki,
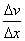 to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz
z głębokością x,
to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz
z głębokością x,
 to współczynnik proporcjonalności pełniący tu rolę
współczynnika lepkości dynamicznej
to współczynnik proporcjonalności pełniący tu rolę
współczynnika lepkości dynamicznej
Korzystając z powyższego wzoru można wyprowadzić wzór, zwany prawem Poiseuille'a
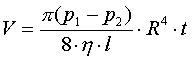
Wzór ten podaje, jaka objętość cieczy o współczynniku lepkości  przepływa w czasie
t przez rurę o promieniu R i długości l, przy różnicy ciśnień na końcach rury p1-p2
przepływa w czasie
t przez rurę o promieniu R i długości l, przy różnicy ciśnień na końcach rury p1-p2
Korzystając z tego wzoru, można określić wielkość siły tarcia na jakie napotyka
ciecz płynąca w rurze z średnią pędkością cząsteczek vśr w przypadku przepływu laminarnego. Siła ta hamuje
prędkość przepływu cieczy.
Wzór ten ma postać:
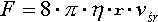
Zlepkością cieczy wiąże się też zjawisko hamowania ruchu ciał poruszających się w lepkiej cieczy.
W przypadku gdy ciałem tym jest kulka, poruszająca się na tyle wolno, aby opływ cieczy był laminarny
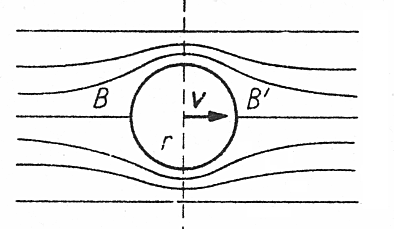
jak na tym rysunku
a nie turbulentny
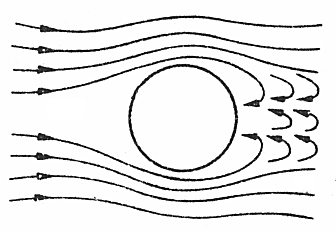
jak na tym rysunku
Siłę tę opisuje prawo Stokesa:
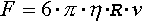
Korzystając z tego wzoru, można łatwo wyprowadzić wzór na prędkość kulki spadającej w lepkiej cieczy.
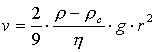
Wyznaczanie bezwzględnego współczynnika lepkości bezpośrednio z tego wzoru jest dość uciążliwe, ze względu na dużą liczbę występujących
w nim wielkości. Aby nieco uprościć tę czynność skonstruowano przyrząd zwany wiskozymetrem Hoepplera.
W wiskozymetrze tym stosuje się kulkę wykonaną z materiału o znanej gęstosci,
której parametry (tzw stałą kulki K) określa się wstępnie w cieczy o znanej lepkości i gęstości.
Teraz znając gęstość dowolnej innej cieczy, możemy wyznaczyć jej lepkość mierząc czas
opadania kulki w tej cieczy na tym samym odcinku co w cieczy wzorcowej.
W tym wypadku zamiast podanego wyżej wzoru korzystamy z wzoru uproszczonego:

We wzorze tym  to współczynnik lepkości badanej cieczy,
t- czas opadania kulki w tej cieczy,
to współczynnik lepkości badanej cieczy,
t- czas opadania kulki w tej cieczy,  to gęstość kulki,
to gęstość kulki,
 1-gęstość cieczy, a K to właśnie stała kulki.
Stałą aktualnie używanej kulki podano w instrukcji znajdującej się na stnowisku. Wyznacza się ją,
mierząc czas opadania tej kulki w wiskozymetrze zawierającym ciecz o znanej lepkości i gęstosci.
1-gęstość cieczy, a K to właśnie stała kulki.
Stałą aktualnie używanej kulki podano w instrukcji znajdującej się na stnowisku. Wyznacza się ją,
mierząc czas opadania tej kulki w wiskozymetrze zawierającym ciecz o znanej lepkości i gęstosci.
 CEL ĆWICZENIA
CEL ĆWICZENIA
Celem ćwiczenia jest wyznaczenie zależności współczynnika lepkości dynamicznej cieczy od temperatury
w oparciu o badanie czasu opadania tej w cieczy kulki o znanych parametrach.
 METODA POMIAROWA
METODA POMIAROWA
Na rysunku poniżej widoczny jest przyrząd służący do pomiarów.

- 1- kulka opadająca w badanej cieczy
- 2- cylinder szklany z badaną cieczą
- 3- obudowa wypełniona wodą pełniącą rolę cieczy termostatującej
- 4- poziomica
- 5- termometr
- 6- zatrzask sprężynowy
- 7,8,9- podłączenia do termostatu
Wiskozymetr podłączony jest do wymuszonego obiegu wody, której temperatura
stabilizowana jest przez ultratermostat z dokładnością do około 0,5 oC.
Umożliwia to wyznaczenie zależności współczynnika lepkości badanej cieczy od temperatury.
Rurka 2 wiskozymetru, w której opada kulka jest odchylona od pionu o ok. 10o, aby zapobiec
wahadłowemu opadaniu kulki, przez co opływ cieczy przestałby być laminarny.
Współczynnik lepkości wyznaczać będziemy z zależności:

W tym celu, po ustabilizowaniu się określonej tempetratury, zmierzymy kilkukrotnie czas opadania
kulki pomiędzy określonymi poziomami
(oznaczonymi na cylindrze kreskami A i B).
Pomiary powtarzamy w kilku temperaturach w zakresie od 25oC do 60 oC.
 OPRACOWANIE WYNIKÓW POMIARÓW
OPRACOWANIE WYNIKÓW POMIARÓW
Dokładny przebieg pomiarów podany jest w instrukcji stanowiskowej
Proponowana tabelka ma postać:

W tabeli tej wpisujemy, wyrażone w kelwinach, temperatury, w których mierzymy czas opadania kulki oraz czasy
opadania kulki. Pozostałe wielkości wpisujemy do tabelki na podstawie podanych w instrukcji stanowiskowej danych.
Gęstość cieczy w danej temperaturze wyliczamy według podanego w instrukcji wzoru:

Na podstawie tabelki należy sporzadzić dwa wykresy:
 oraz
oraz 
Pierwszy przedstawia po prostu przebieg zmian lepkości badanej cieczy w funkcji temperatury
- powinien być fragmentem pewnej funkcji wykładniczej:

Dlatego punkty drugiego wykresu powinniśmy dopasować do prostej, najlepiej metodą regresji liniowej,
aby na podstawie współczynnika kierunkowego (a) tej prostej wyznaczyć wartość energii aktywacji E
 OPIS TEORETYCZNY
OPIS TEORETYCZNY OPIS TEORETYCZNY
OPIS TEORETYCZNY


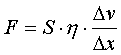
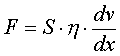
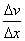 to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz
z głębokością x,
to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz
z głębokością x, to współczynnik proporcjonalności pełniący tu rolę
współczynnika lepkości dynamicznej
to współczynnik proporcjonalności pełniący tu rolę
współczynnika lepkości dynamicznej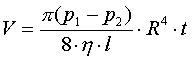
 przepływa w czasie
t przez rurę o promieniu R i długości l, przy różnicy ciśnień na końcach rury p1-p2
przepływa w czasie
t przez rurę o promieniu R i długości l, przy różnicy ciśnień na końcach rury p1-p2
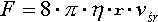


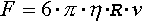
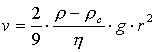

 to współczynnik lepkości badanej cieczy,
t- czas opadania kulki w tej cieczy,
to współczynnik lepkości badanej cieczy,
t- czas opadania kulki w tej cieczy,  to gęstość kulki,
to gęstość kulki,
 1-gęstość cieczy, a K to właśnie stała kulki.
Stałą aktualnie używanej kulki podano w instrukcji znajdującej się na stnowisku. Wyznacza się ją,
mierząc czas opadania tej kulki w wiskozymetrze zawierającym ciecz o znanej lepkości i gęstosci.
1-gęstość cieczy, a K to właśnie stała kulki.
Stałą aktualnie używanej kulki podano w instrukcji znajdującej się na stnowisku. Wyznacza się ją,
mierząc czas opadania tej kulki w wiskozymetrze zawierającym ciecz o znanej lepkości i gęstosci.
 CEL ĆWICZENIA
CEL ĆWICZENIA METODA POMIAROWA
METODA POMIAROWA

 OPRACOWANIE WYNIKÓW POMIARÓW
OPRACOWANIE WYNIKÓW POMIARÓW

 oraz
oraz 
