Z faktu, że ciecz jest praktycznie nieściśliwa wynika, że prędkość cieczy
w miejscach o mniejszym przekroju jest większa, niż w miejscu o przekroju większym (gdy ciecz wypełnia całą rurę).
Po prostu tyle samo cieczy musi przepłynąć przez dowolny przekrój.
Opisuje to prawo ciągłości przepływu
 ,
,
które mówi, że w dowolnym miejscu rury iloczyn prędkości cieczy i pola powierzchni przekroju rury jest
taki sam. Zatem w jednostce czasu, przez dowolny przekrój rury przepływa tyle samo cieczy.
Dla przepływu cieczy nieściśliwej ma zastosowanie równanie Bernoulliego które mówi, że dla dowolnego odcinka przewodu z cieczą,
całkowite ciśnienie jest stałe.
Ciśnienie to jest sumą ciśnienia statycznego p,
ciśnienia hydrostatycznego  (h- to różnica wysokości słupa cieczy),
oraz ciśnienia dynamicznego
(h- to różnica wysokości słupa cieczy),
oraz ciśnienia dynamicznego 
(v- to prędkość cieczy).

Wskutek lepkości prędkość cieczy w całym przekroju rury nie jest stała, lecz zmienia się od zera (v=0) przy ściankach, do
maksymalnej wartości w środku rury. Jeżeli przepływ jest laminarny, to rozkład prędkości ma symetrię osiową i zależy tylko
od odległości r od osi rury. Aby określić prędkość przepływu cieczy w różnych miejscach i ilość cieczy przepływającej
przez rurę w określonym czasie, rozważę ruch porcji wody w kształcie walca o długości l, płynącej w rurze o promieniu R.

Na powierzchnię boczną wybranego walca działa siła

Wskutek różnicy ciśnień na końcach walca na tę porcję cieczy działa siła P:

Skoro przepływ cieczy jest stacjonarny (prędkość cieczy nie zmienia się w czasie),
wszystkie siły się równoważą , czyli siła P równa jest sile lepkości (P= -F):

Zatem 
i 
Całkując znajdujemy prędkość cieczy.

Stałą całkowania C wyznaczamy z warunku, że v(R)=0:

I tak otrzymujemy wzór na prędkość cieczy w zależności od odległości od osi rury:

Warto zauważyć, że z wzoru tego wynika, iż rozkład prędkości ma kształt paraboli:
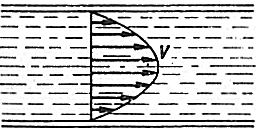
W czasie t przez pierścień o promieniu r i szerokości dr przepływa ilość
cieczy zajmująca objętość dV:

Przez całą rurę przepłynie w tym czasie:

Całkowanie daje nam ostecznie wynik

Równanie to nosi nazwę prawa Hagena-Poiseuille'a
Korzystając z prawa Hagena-Poiseuille'a można wyprowadzić średnią prędkość laminarnego przepływu
cieczy w rurze:

W przypadku ruchu ustalonego (vśr=0) siła P= S p
wynikająca z różnicy ciśnień
p
wynikająca z różnicy ciśnień  p równoważy siłę tarcia F.
p równoważy siłę tarcia F.
Z powyższego wzoru na prędkość średnią otrzymamy zatem:

Tak więc ciecz płynąca w rurze o promieniu R i długości l, napotyka na siłę oporu związaną z lepkością
cieczy równą:
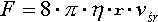
Na kulę poruszającą się w lepkiej cieczy z prędkością v taką, aby ruch cieczy względem kuli był laminarny
(jak na rysunku):
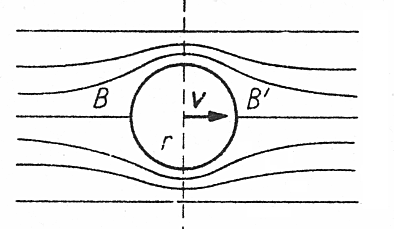
działa siła wyrażona wzorem Stokesa:
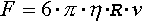
Rozważmy przypadek małej kulki o promieniu r spadającej w lepkiej cieczy.
Na kulkę tę działają trzy siły:

Q- siła ciężkości;
Fw- siła wyporu;
 -siła lepkości
-siła lepkości
Siły te wyrazić można wzorami:



Na początku ruchu siła ciężkości jest większa od sumy pozostałych sił zgodnie z równaniem:

i kulka porusza się ruchem przyspieszonym (niejednostajnie).
Ponieważ jednak wraz ze wzrostem prędkości rośnie siła lepkości (dwie pozostałe siły są stałe),
dochodzi wkrótce do momentu, gdy suma sił w powyższym równaniu staje się równa zeru:

Jak wiemy z I zasady dynamiki :
("jeżeli na ciało nie działa żadna siła, lub działające siły równoważą się, to ciało pozostaje w spoczynku lub
porusza się ruchem jednostajnym prostoliniowym")
od tej chwili kulka będzie poruszać się ze stałą prędkością, którą
wyznaczamy z powyższego równania:

Stąd wzór na prędkość kulki:

Z tego wzoru wynika, że małe kulki uzyskują mniejszą prędkość niż duże. Dlatego np. małe kropelki deszczu opadają
w powietrzu dużo wolniej niż duże.
Wzór ten może posłużyć do wyznaczania lepkości cieczy lub gazu w oparciu o pomiar prędkości
opadania kulki o znanym promieniu.
Funkcja wykładnicza:

opisuje przybliżoną zależność lepkości cieczy od temperatury. W wykładniku tego wyrażenia wystepuje tzw. energia aktywacji E.
W uproszczeniu jej sens można wyjasnić w następujący sposób: wzajemne przemieszczanie się w cząstek w lepkiej cieczy nie zachodzi swobodnie lecz
z pewnym utrudnieniem. Cząstka taka zanim się przemiesci w nowe położenie trwa przez jakiś czas w pewnym
chwilowym położeniu równowagi, wykonując zwykłe drgania termiczne (podobnie jak w ciele stałym). Po pewnym czasie (tzw. czasie relaksacji) czastka przeskakuje
w inne położenie itd. Aby jednak cząstka mogła zająć to inne położenie musi wytworzyć się (wskutek drgania innych cząstek) tzw. wnęka cząsteczkowa
czyli miejsce dla tej cząsteczki.
Energia potrzebna na wytworzenie takiej wnęki jest właśnie tą energią aktywacji.
Jest ona zależna od ciśnienia cieczy i w pewnym stopniu od temperatury cieczy.

 (h- to różnica wysokości słupa cieczy),
oraz ciśnienia dynamicznego
(h- to różnica wysokości słupa cieczy),
oraz ciśnienia dynamicznego 















 p
wynikająca z różnicy ciśnień
p
wynikająca z różnicy ciśnień  p równoważy siłę tarcia F.
p równoważy siłę tarcia F.
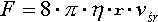

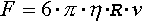

 -siła lepkości
-siła lepkości 






