Wyznaczanie momentu bezwładności za pomocą przyrządu Hartle'a

OPIS TEORETYCZNY

Do opisu ruchu obrotowego bryły sztywnej . należy uwzględnić wielkości nieistotne przy opisie ruchu postępowym ciała. W tym wypadku bowiem rozmiary bryły, przestrzenny rozkład masy a także oś, względem której może się ona obracać odgrywają istotne znaczenie. I dlatego:

do określenia bezwładności bryły nie wystarczy podanie tylko jej masy, lecz należy zdefiniować moment bezwładności I
każdy punkt obracającej się bryły ma inną prędkość liniową, zatem niezbędne staje się wprowadzenie pojęcia prędkości kątowej , która jest wspólna dla całej bryły.
energia kinetyczna obracającej się bryły zależy nie tylko od masy ciała i prędkości poruszania się środka masy bryły, ale również od prędkości kątowej bryły i jej momentu bezwładności względem osi obrotu.

Korzystając z definicji momentu bezwładności można, bez bez większego trudu, wyprowadzić wzór na moment bezwładności dla kilku regularnych brył, szczególnie dla jednorodnych brył obrotowych. Również w literaturze można spotkać przykłady takich wzorów. Jednak, aby wyznaczyć moment bezwładności konkretnego ciała, trzeba uciec się często do doświadczenia. Przykładem przyrządu służącego do doświadczalnego wyznaczenia momentu bezwładności jest przyrząd Hartle'a.

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie momentu bezwładności kilku tarcz metalowych i sprawdzenie czy otrzymane wyniki zgadzają się z obliczonymi na podstawie teoretycznego wzoru.

METODA POMIAROWA

Układ pomiarowy składa się z:

umocowanego na poziomej osi bloku A, na który nawinięta jest nić
zestawu metalowych tarcz B, które można mocować na osi bloku A
dwóch odważników o znanych masach m₁
i m₂, wieszanych na końcu nici i wprawiających w ruch obrotowy blok i badane tarcze,
podziałki milimetrowej służącej do pomiaru drogi przebywanej przez opadający ciężarek,
układu elektronicznego pomiaru czasu trwania ruchu o dokładności 0,01s.

Idea pomiaru polega na zamianie energii potencjalnej odważnika (zawieszonego na nici nawiniętej na bloku i opadającego pod wpływem siły ciężkości) na energię kinetyczną. Na tę energię kinetyczną składa się na energia kinetyczna ruchu postępowego odważnika i energia kinetyczna ruchu obrotowego bloku z tarczą. Część tej energii potencjalnej jest, niestety, tracona na wykonanie pracy przeciwko siłom tarcia T. Aby wyeliminować tę, niewygodną do wyznaczenia, stratę, wykonujemy dla każdej tarczy pomiary przy użyciu dwóch różnych odwazników o znanych masach m₁ i m₂. Oznaczając odpowiednio symbolami:
E_ko -energię kinetyczną odważnika na nitce,
E_kb -sumę energii kinetycznej bloku z nicią i tarczy
E_p -energię potencjalną odważnika na nitce,
W_T -pracę sił tarcia hamującego ruch (tarcie w osi bloku, tarcie nici o blok itp.),
Zasadę zachowania energii możemy zapisać dla tego układu następująco:

Podstawiając odpowiednie wzory i uwzględniając to, że praca sił tarcia przy niewiele różniących się masach odważników jest praktycznie taka sama, otrzymamy dla odważników m₁ i m₂ dwa równania:

Po odjęciu stronami i przekształceniu otrzymamy na moment bezwładności wzór:

Korzystając ze wzoru na związek prędkości kątowej z liniową:

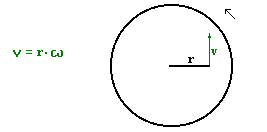
a następnie na drogę ciężarka w ruchu jednostajnie przyspieszonym, z prędkością początkową równą zero

wyeliminujemy trudne do bezpośredniego pomiaru prędkości v i

, otrzymując ostatecznie zależność:

CZYNNOŚCI POMIAROWE

Wyznaczamy masy wszystkich badanych tarcz
Mierzymy średnice bloku i wszystkich badanych tarcz i obliczamy ich promienie (odpowiednio r i R)
Dla każdej tarczy mierzymy czasy t₁ i t₂ opadania ciężarków m₁ i m₂ na ustalonym odcinku drogi h. Należy pamiętać, aby rozpoczynać pomiary czasu od prędkości początkowej odważnika równej zero.
Pomiary dla każdej tarczy i każdego odważnika przeprowadzamy co najmniej trzykrotnie.
Pomiary opisane w punkcie 3 powtórzyć bez tarcz, aby wyznaczyć moment bezwładności bloku i pozostałych niezmiennych części układu.

OPRACOWANIE WYNIKÓW POMIARÓW

Pomiary umieszczamy w tabeli takiej jak w instukcji:
Instrukcja

Należy sporządzić wykres zależności I = f(R²). (W tym celu od całkowitego momentu bezwładności I_c odejmujemy moment I_o bloku i pozostałych niezmiennych, ruchomych czjęści układu.) W tym układzie współrzędnych wykres ten powinien być linią prostą. Rysujemy ją korzystając z metody najmniejszych kwadratów. Oczekiwany współczynnik kierunkowy uzyskanej prostej wynosi a =0,5 (wynika to ze wzoru na moment bezwładności walca). Współczynnik b tej prostej powinien wyrażać moment bezwładności bloku i pozostałych niezmiennych, ruchomych części układu.
Należy dokonać oceny zgodności tego współczynnika (uzyskanego w wyniku realnych pomiarów) z wielkością oczekiwaną w wyniku rozważań teoretycznych. Ocena ta powinna wynikać z obliczonych odchyleń standardowych S_a i S_b współczynników wyznaczonej prostej.
Należy także obliczyć bład maksymalny momentów bezwładności obliczonych ze wzoru I=0,5mR².