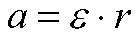Sprawdzanie podstawowego równania dynamiki ruchu obrotowego
Sprawdzanie podstawowego równania dynamiki ruchu obrotowego
OPIS TEORETYCZNY
Wymienione w tytule podstawowe równanie dynamiki ruchu obrotowego to
druga zasada dynamiki ,
która stosuje się nie do ruchu postępowego punktu materialnego ,
lecz do ruchu obrotowego bryły sztywnej .
Do opisu ruchu bryły sztywnej trzeba wprowadzić zupełnie nowe pojęcia,
ponieważ oprócz ruchu postępowego może ona dodatkowo obracać się wokół własnej
osi, a więc w opisie tego ruchu rozmiary bryły, przestrzenny rozkład masy a
także oś, względem której może się ona obracać odgrywają istotne znaczenie.
I dlatego:
- do określenia bezwładności bryły nie wystarczy podanie tylko jej masy,
lecz należy zdefiniować tzw
moment bezwładności I ,
- określenie siły działającej na bryłę nie da nam wystarczającej informacji o
oddziaływaniu na nią, trzeba bowiem znać działający
moment siły M
- każdy punkt obracającej się bryły ma inne przyspieszenie liniowe, zatem
niezbędne staje się wprowadzenie pojęcia
przyspieszenia kątowego ,
które jest wspólne dla całej bryły.
Gdy poznamy w.w. pojęcia, wówczas możemy sformułować
drugą zasadę dynamiki dla ruchu obrotowego.
Równanie to opisuje tylko ruch obrotowy ciała. Do opisu ruchu postępowego bryły
sztywnej stosuje się zwykłe równania dynamiki ruchu postępowego,
a więc uwzględniające masę, działające siły i uzyskane przez ciało pod ich
wpływem przyspieszenie liniowe, lecz odnoszące się tylko do jednego, konkretnego punktu ciała,
a mianowicie do jego środka cieżkości.
CEL ĆWICZENIA
Celem ćwiczenia jest sprawdzenie słuszności podstawowego równania
dynamiki ruchu obrotowego. Nie będzie to jednak sprawdzenie bezpośrednie,
czyli przez pomiar wielkości momentów sił, momentów bezwładności
czy przyspieszeń katowych, ale poprzez sprawdzenie wynikajacych z tego równania
konsekwencji.
METODA POMIAROWA
Doświadczenie przeprowadzamy przy pomocu zestawu pomiarowego, którego schemat
przedstawiony jest na rysunku:
 W układzie tym naszą bryłą sztywną jest blok A ( na który nawinięta jest nić)
wraz z umocowanym na wspólnej osi prętem P i umieszczonymi na tym pręcie
dwiema kulami K.
Kule te można przesuwać po pręcie, zmieniając w ten sposób moment bezwładności
całej bryły. Na drugim końcu nici zawieszony jest odważnik Q, który opadając
ruchem jednostajnie przyspieszonym (a = const) wprawia w ruch obrotowy, (także
jednostajnie przyspieszony, bo
W układzie tym naszą bryłą sztywną jest blok A ( na który nawinięta jest nić)
wraz z umocowanym na wspólnej osi prętem P i umieszczonymi na tym pręcie
dwiema kulami K.
Kule te można przesuwać po pręcie, zmieniając w ten sposób moment bezwładności
całej bryły. Na drugim końcu nici zawieszony jest odważnik Q, który opadając
ruchem jednostajnie przyspieszonym (a = const) wprawia w ruch obrotowy, (także
jednostajnie przyspieszony, bo  = const) całą bryłę.
= const) całą bryłę.
W układzie tym łatwo dają wyznaczyć się:
- masa m odważnika Q,
- droga s przebywana przez odważnik,
- czas ruchu t
- odległość między kulami d.
Należy więc wykazać jakie zależności między wymienionymi wielkościami wynikają z
zasad dynamiki i tak wyprowadzone zależności będziemy następnie sprawdzać.
Na początek zbadamy zależność między czasem t opadania ciężarka
(na jakimś stałym odcinku drogi s) a odległością d kul na pręcie.
W równaniu
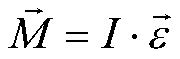
moment bezwładności I
jest sumą stałej wielkości Io ( na nią składają się momenty
bezwładności bloku A, pręta P i każdej z kul względem własnej osi)
oraz momentu bezwładności obu kul względem osi całego układu.
(Trzeba tu skorzystać m.in. z twierdzenia
Steinera ).
Czyli

m oznacza tutaj masę jednej kulki.
Ruch obrotowy układu wywołuje bezpośrednio siła naprężenia nici N, której
moment, pomniejszony o pewien moment sił tarcia w osi
bloku, nadaje układowi pewne przyspieszenie kątowe 
( Uwaga: moment siły tarcia zależy tu bezpośrednio od promienia samej osi, a nie
całego krążka jak błednie przyjęto w skrypcie "Ćwiczenia laboratoryjne z
fizyki").
 Całą naszą wiedzę o układzie doświadczalnym możemy więc zawrzeć w następującym
układzie równań:
Całą naszą wiedzę o układzie doświadczalnym możemy więc zawrzeć w następującym
układzie równań:

- Druga zasada dynamiki zastosowana do odważnika Q

- Druga zasada dynamiki ruchu obrotowego (patrz rysunek powyżej)

- Moment bezwładności całego układu

- Moment siły naprężenia
 nici pomniejszony o moment sił
tarcia w osi bloku, wywołujący ruch obrotowy
nici pomniejszony o moment sił
tarcia w osi bloku, wywołujący ruch obrotowy

- Związek między przyspieszeniem kątowym a przyspieszeniem liniowym
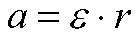
- Droga ciężarka Q w ruchu jednostajnie przyspieszonym, z prędkością początkową równą zero

Wykonując proste przekształcenia matematyczne wyznaczamy przyspieszenie a
z równań 1 do 5
i porównujemy je z przyspieszeniem wyliczonym ze
wzoru 6, otrzymując ostatecznie na czas wzór
:

a stąd

Ponieważ poza czasem i odległością między kulami przyjęliśmy pozostałe wielkości
za stałe, otrzymamy równanie

Symbolami c i b oznaczyłem tutaj stałe odpowiednio

Jeśli sporządzimy więc wykres zależności t2 od
d2, to powinniśmy otrzymać na wykresie linię prostą.
Na otrzymaniu linii prostej na tym wykresie będzie więc polegało (zawarte w
temacie ćwiczenia) sprawdzenie podstawowego równania dynamiki ruchu
obrotowego.
Drugim sposobem sprawdzenia tego równania jest sporządzenie zależności między
zmienną masą odważnika, a czasem opadania odważnika przy zachowaniu stałej
odległości między kulkami i stałej drogi opadania.
W tym wypadku z wzoru (*) otrzymamy

czyli zależność postaci:

gdzie stałe k i A wynosza:

I tu także rysując wykres 1/t2 od m powinniśmy otrzymać
prostą jako potwierdzenie tytułowego równania.
Na koniec, aby sprawdzić czy słuszne było nasze, przyjęte w punkcie 6,
założenie, że ruch jest jednostajnie przyspieszony, zbadamy zależność
t2 od s. Także ta zależność powinna być liniowa.
WYKONANIE POMIARÓW
A. Badanie zależności t2 od s:
Wybieramy do pomiarów jeden z odważników i ustalamy stałą dla wszystkich
pomiarów odległość między kulkami. Zmieniamy drogę s i mierzymy czas
t. Wyniki umieszczamy w tabeli:
TABELA 1
B. Badanie zależności 1/t2 od m:
Wybieramy do wszystkich pomiarów stały odcinek drogi i pozostawiamy stałą
odległość między kulkami. Wybieramy odważniki o różnych masach m
i mierzymy czas t. Wyniki umieszczamy w tabeli:
TABELA 2
C. Badanie zależności t2 od d:
Wybieramy do pomiarów jeden z odważników i ustalamy stałą dla wszystkich
pomiarów drogę. Zmieniamy odległość między kulkami i mierzymy czas.
Wyniki umieszczamy w tabeli:
TABELA 3
OPRACOWANIE WYNIKOW POMIARÓW
Rysujemy wykresy opisane w punktach A, B, C.
Proste wyznaczamy stosując metodę regresji liniowej i obliczając
odchylenia standardowe współczynników prostych
Sa i Sb.
 Sprawdzanie podstawowego równania dynamiki ruchu obrotowego
Sprawdzanie podstawowego równania dynamiki ruchu obrotowego Sprawdzanie podstawowego równania dynamiki ruchu obrotowego
Sprawdzanie podstawowego równania dynamiki ruchu obrotowego
 = const) całą bryłę.
= const) całą bryłę.
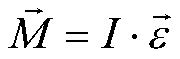







 nici pomniejszony o moment sił
tarcia w osi bloku, wywołujący ruch obrotowy
nici pomniejszony o moment sił
tarcia w osi bloku, wywołujący ruch obrotowy