 Wyznaczanie współczynnika tarcia tocznego za pomocą wahadła nachylnego.
Wyznaczanie współczynnika tarcia tocznego za pomocą wahadła nachylnego.
 Wyznaczanie współczynnika tarcia tocznego za pomocą wahadła nachylnego.
Wyznaczanie współczynnika tarcia tocznego za pomocą wahadła nachylnego.

Siły tarcia poślizgowego hamują ruch posuwisty jednego ciała względem drugiego
głównie dzięki temu, że stykające się powierzchnie trących ciał zazębiają się o
siebie nierównościami (czasami niewidocznymi gołym okiem), powodując nieustanne ścieranie się tych powierzchni.
Dodatkowo, przy niewielkiej chropowatości powierzchni, zwiększa się rola,
zachodzących na poziomie mikroskopowym:
-
różnorodnych oddziaływań elektrostatycznych między cząsteczkami
(tzw adhezja czyli przyleganie),
- dyfuzji
a nawet
- powierzchniowych reakcji chemicznych.
Obecność sił tarcia poślizgowego hamuje i
utrudnia przesuwanie jednego ciała po drugim. Natomiast obecność tych sił jest
niezbędna przy toczeniu (a więc np. przy ruchu wszelkich pojazdów kołowych),
gdyż to właśnie moment siły tarcia
wywołuje ruch obrotowy.
Tak więc siły tarcia niezbędne są, aby zachodziło toczenie, z drugiej
strony toczenie ciała jest hamowane przez inne tarcie, o zupełnie innej
naturze, mianowicie przez tarcie toczne.
Występowanie tarcia tocznego wiąże się z plastycznym odkształceniem powierzchni,
po której toczy się ciało cylindryczne lub kuliste i samej powierzchni
toczącego się ciała. Najlepiej wyjaśnić to na podstawie dwóch kolejnych
rysunków :
Pierwszy przedstawia sytuację, kiedy tarcie toczne nie występuje w
ogóle, drugi wyjaśnia działanie hamujące ruch obrotowy.

Spoczywający walec lub walec idealnie sprężysty toczący się po idealnie
sprężystym podłożu powoduje symetryczne odkształcenia, a więc wypadkowe siły
F1, F2
działające na obie stykające się z podłożem części kuli są równe i działają
symetrycznie względem pionowej płaszczyzny AA' przechodzącej przez oś
obrotu. Siły te tworzą w sumie wypadkową siłę R- reakcji podłoża na
nacisk, która przechodzi przez oś obrotu. Zatem moment tej siły jest równy zeru
i nie może ona (zgodnie z
II zasadą dynamiki dla ruchu obrotowego )
zmienić prędkości obrotowej toczącego się ciała.
(Bo przyspieszenie kątowe równe jest zeru).

W rzeczywistości nie ma tak do końca idealnie sprężystych odkształceń. A wtedy
okazuje się, że siły reakcji podłoża F2 od strony, na którą
naciera toczące się ciało są większe od sił działających z przeciwnej strony, a
co więcej nie działają one symetrycznie (kierunek siły z prawej strony pzebiega
ponad osią ciała, zaś siły z lewej strony poniżej osi).
Z tych powodów wypadkowa siła R (reakcji podłoża na nacisk) nie
przechodzi przez oś obrotu i wywiera na toczące się ciało niezerowy moment siły.
Moment ten zmniejsza prędkość kątową, a więc prędkość toczenia się ciała.
O ile więc przy ruchu posuwistym hamujący wpływ na ruch ma siła
wynikająca z
nacisku ciała na podłoże, o tyle przy toczeniu istotne znaczenie ma
moment siły związany z tą siłą.
Rzeczywiste toczące się ciała nigdy nie stykają się tylko jednym punktem z
powierzchnią, po której toczą się, niemniej powierzchnia ich styku z podłożem
jest na ogół bardzo niewielka. Siła R jest więc na ogół "prawie" pionowa.
Kąt między tą siłą a kierunkiem pionu (oznaczmy go 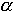 ) jest
więc niewielki, bliski zera. Na rysunku poniżej, dla uzyskania większej
przejrzystości, jest on nieproporcjonalnie duży.
) jest
więc niewielki, bliski zera. Na rysunku poniżej, dla uzyskania większej
przejrzystości, jest on nieproporcjonalnie duży.

Jeśli wypadkową siłę R rozłożymy na składowe
otrzymamy siłę pionową N równoważącą siłę nacisku ciała na podłoże oraz
siłę poziomą Ft, której moment jest właśnie przyczyną
hamowania ruchu obrotowego. Rozważmy przypadek skrajnie małego tarcia tocznego,
gdy kula toczy się "prawie" ruchem jednostajnym (jej przyspieszenie kątowe równe jest
zero) pod wpływem pewnej zewnętrznej siły F. Wówczas moment siły Ft i moment siły N muszą
być równe (toczenie nie jest hamowane).
Moment siły tarcia Ft wynosi:

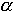 w porównaniu do kąta 90o jest mały można go zaniedbać,
a sin90o = 1 ).
w porównaniu do kąta 90o jest mały można go zaniedbać,
a sin90o = 1 ). 


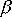 .
.
 h niżej i jej energia maleje o pewną wartość
h niżej i jej energia maleje o pewną wartość



 l oznacza tu odległość poziomą między położeniami kulki
odpowiadającymi zmianie jej wysokości o
l oznacza tu odległość poziomą między położeniami kulki
odpowiadającymi zmianie jej wysokości o  h.
h.


 l oraz s nie jest zbyt wygodny,
przekształcimy nieco ten wzór tak, aby wyrazić je przez łatwo mierzalne
wielkości. Po kilku przekształceniach
otrzymamy końcowy wzór:
l oraz s nie jest zbyt wygodny,
przekształcimy nieco ten wzór tak, aby wyrazić je przez łatwo mierzalne
wielkości. Po kilku przekształceniach
otrzymamy końcowy wzór:

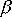 lecz kąt
lecz kąt 
 = 90o-
= 90o-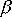 ),
końcowy wzór przyjmie postać:
),
końcowy wzór przyjmie postać:

 (np. 30o)
(np. 30o)
 i
puszczamy ją
i
puszczamy ją
 n-tego (np. n= 10) wychylenia kulki.
Tego odczytu musimy dokonać "w biegu", w czasie ruchu kulki
n-tego (np. n= 10) wychylenia kulki.
Tego odczytu musimy dokonać "w biegu", w czasie ruchu kulki
 i dla różnych płytek, po których toczy się kulka.
i dla różnych płytek, po których toczy się kulka.