Pomiar długości fali światła
za pomocą siatki dyfrakcyjnej. (413)
OPIS TEORETYCZNY.
Udowodniono, że światło można traktować
zarówno jako zbiór cząstek (fotonów)
wylatujących ze źródła światła
i poruszających się po liniach prostych (korpuskularna
teoria światła wyjaśniająca np. bardzo dobrze
zjawisko fotoelektryczne
czy efekt Comptona), jak też jako falę z wszystkimi
charakterystycznymi dla niej własnościami
(np. dyfrakcja, interferencja, polaryzacja).
W tym drugim ujęciu światło jest falą elektromagnetyczną,
poprzeczną, rozchodzącą się
w przestrzeni z bardzo dużą predkością.
Natrafiając na przeszkodę, światło ulega
ugięciu czyli dyfrakcji
i zmienia kierunek rozchodzenia się.
Zjawisko to można wyjasnić np. w oparciu o zasadę Huygensa.
Otóż w wypadku natrafienia na przeszkodę, czoła
niektórych cząstkowych
fal kulistych nie mogą rozchodzić się swobodnie
w niektórych kierunkach. Zatem
powstała w wyniku interferencji fal
cząstkowych powierzchnia styczna do tych fal (czoło
fali wypadkowej) także zmieni swój kształt
Zatem kierunek rozchodzenia się fali także ulegnie zmianie.
Zjawisko dyfrakcji i interferencji szczególnie wyraźnie
można zaobserwować przy
przejściu światła przez układ wąskich
szczelin. Po przejściu przez jedną, wąską
szczelinę,
światło rozchodzące się prostoliniowo (fala
płaska), zmienia się w falę kulistą,
rozchodzącą się we wszystkich kierunkach.
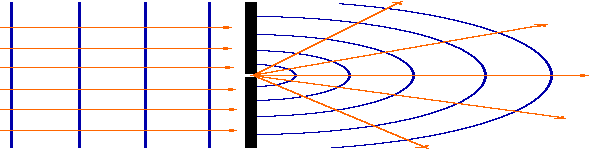
Jeśli szczeliny będą dwie, sytuacja zmieni się,
gdyż wiązki światła wychodzące z różnych
szczelin będą się spotykać, a ponieważ
są spójne
, interferują ze sobą.
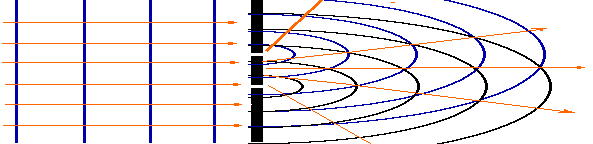
Jeśli za szczelinami ustawimy
ekran, zaobserwujemy na nim szereg
jasnych punkcików - prążków interferencyjnych.
Powstaną one w tych miejscach,
w których wiązki wychodzące z różnych
szczelin spotkają się w zgodnej fazie.

Określenie położenia tych punktów jest proste.
W fali padającej
powierzchnia falowa dochodzi
równocześnie do obu szczelin więc wychodzące
ze szczelin wiązki są w tej samej fazie.
Zatem na ekranie fale spotkają się w zgodnej fazie
wtedy, gdy przebędą tę samą drogę
optyczną (k=0) albo gdy przebyte przez nie drogi będą
różnić się o całkowitą wielokrotność
długości fali 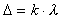 (k=0,1,2...).
(k=0,1,2...).

Taki układ szczelin można potraktować jako przybliżony
model siatki dyfrakcyjnej.
Rzeczywista siatka dyfrakcyjna składa się z wielu szczelin.
Często przypada ich
kilkaset na jeden milimetr szerokości siatki. Odległość
między sąsiednimi szczelinami
(na rysunku oznaczona jako d ) nazywana jest
stałą siatki.
Z rysunku widać, że kąt 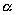 , pod którym zaobserwujemy wzmocnienie interferencyjne
(jasny prążek) i kąt B w trójkącie
ABC są równe. (Uwaga. Na rysunku nie jest
zachowana skala. W rzeczywistości odległość
między szczelinami d= AB << L (L to odległość między szczelinami a ekranem), dzięki czemu obie wiązki
wychodzą jakby -w tej skali- z tego samego punktu).
, pod którym zaobserwujemy wzmocnienie interferencyjne
(jasny prążek) i kąt B w trójkącie
ABC są równe. (Uwaga. Na rysunku nie jest
zachowana skala. W rzeczywistości odległość
między szczelinami d= AB << L (L to odległość między szczelinami a ekranem), dzięki czemu obie wiązki
wychodzą jakby -w tej skali- z tego samego punktu).
Z zależności geometrycznych widać że:
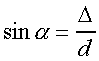
oraz
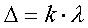
Otrzymujemy stąd tzw równanie siatki dyfrakcyjnej:
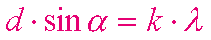
Położenie prążków na ekranie określa
zależność:
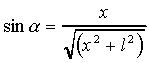
Kojarząc powyższe wzory otrzymujemy zależność,
w oparciu o którą można
doświadczalnie wyznaczyć długość fali
światła:
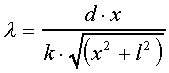
Bardzo elegancką ilustrację zjawiska interferecji możesz obejrzeć
jeśli dysponujesz komputerem w miarę szybkim i z co najmniej 12MB RAM.
Skocz tutaj
METODA POMIAROWA.
Do doświadczenia należy użyć źródła
światła monochromatycznego.
W naszym przypadku będzie to miniaturowy laser półprzewodnikowy,
wysyłający światło
czerwone. Laser oświetla bezpośrednio siatkę dyfrakcyjną
równoległą wiązką
promieni, a prążki interferencyjne obserwujemy na ekranie,
na tle skali milimetrowej.
środkowy prążek, zwany prążkiem zerowym
(odpowiada k=0),służy za punkt
odniesienia do pomiaru odległości x
dla prążków wyższych rzędów.
Dla siatki, którą dysponujemy na pracowni (stała
siatki d= 0,005mm czyli 200 szczelin/mm) i dla światła
danej długości możemy zaobserwować maksymalnie
prążki trzeciego rzędu (k=3).
CEL ĆWICZENIA.
Celem ćwiczenia jest wyznaczenie długości fali
światła monochromatycznego,
poprzez pomiar ugięcia światła na transmisyjnej
siatce dyfrakcyjnej o znanej stałej
siatki.
WYKONANIE ĆWICZENIA.
Włączamy laser i ustawiamy laser i siatkę w statywie
w taki sposób, aby na ekranie były
widoczne prążki interferencyjne na tle skali. Należy
zadbać o to, aby siatka i ekran były
ustawione równolegle względem siebie. (Laser jest
na stałe zamocowany tak, aby światło
padało na siatkę prostopadle. Ważne!)
Mierzymy odległość od siatki do ekranu oraz odległości
od prążka zerowego
do prążków I, II i III rzędu. Pomiary
przeprowadzamy zarówno dla prążków leżących
z lewej jak i z prawej strony prążka centralnego, notując
za każdym razem rząd prążka.
Podobne pomiary powtarzamy dla czterech innych odległości
między siatką a ekranem.
Wyniki umieszczamy w tabeli:
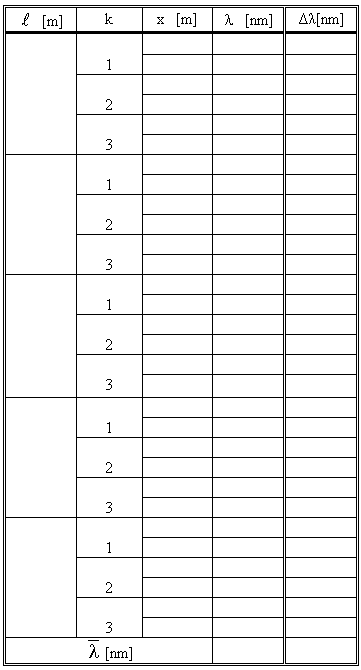
OPRACOWANIE WYNIKÓW POMIARÓW.
Należy obliczyć długości fali wynikających
z pomiarów poszczególnych prążków
ze wzoru :
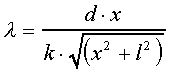
Nastepnie znaleźć wartość średnią
długości fali oraz określić niepewność
pomiaru
Każdy pomiar długości fali w tym ćwiczeniu przeprowadzany
jest z inną dokładnością i dlatego, aby pomiary bardziej dokładne miały większy
wpływ na wyniki niż pomiary mniej dokładne należy jako średnią długość fali przyjąć
tzw. średnią arytmetyczną ważoną.
Jako wagę danego pomiaru należy przyjąć wielkość odwrotnie
proporcjonalną do kwadratu błędu pomiaru, czyli wyrażenie typu
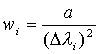
Stała "a" jest tu zupełnie dowolna i wygodnie jest w tym
wypadku przyjąć ją jako a=10-9, ponieważ długość fali wyrażać
będziemy w nanometrach.
Niepewności 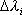 obliczamy jako błędy
maksymalne pomiarów pośrednich metodą różniczki zupełnej:
obliczamy jako błędy
maksymalne pomiarów pośrednich metodą różniczki zupełnej:
- obliczamy pochodną d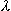 z funkcji
z funkcji
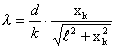
wynosi ona:

- zamieniamy "-" na "+" i ostatecznie więc niepewność
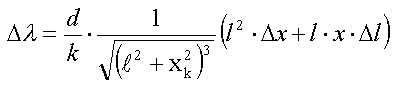
Po obliczeniu wszystkich niepewności 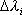 obliczamy średnią ważoną długość fali wg wzoru :
obliczamy średnią ważoną długość fali wg wzoru :
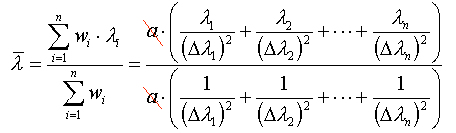
A następnie błąd maksymalny średniej ważonej:
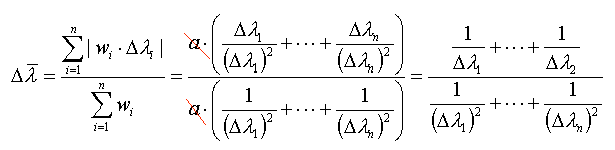
Wynik przedstawić w postaci:
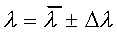
UWAGA
Można tu także ściągnąć pełną postać instrukcji stanowiskowej zapisaną w formacie WORD-a
Powrót do
 Strony tytułowej
Strony tytułowej




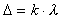 (k=0,1,2...).
(k=0,1,2...).

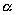 , pod którym zaobserwujemy wzmocnienie interferencyjne
(jasny prążek) i kąt B w trójkącie
ABC są równe. (Uwaga. Na rysunku nie jest
zachowana skala. W rzeczywistości odległość
między szczelinami d= AB << L (L to odległość między szczelinami a ekranem), dzięki czemu obie wiązki
wychodzą jakby -w tej skali- z tego samego punktu).
, pod którym zaobserwujemy wzmocnienie interferencyjne
(jasny prążek) i kąt B w trójkącie
ABC są równe. (Uwaga. Na rysunku nie jest
zachowana skala. W rzeczywistości odległość
między szczelinami d= AB << L (L to odległość między szczelinami a ekranem), dzięki czemu obie wiązki
wychodzą jakby -w tej skali- z tego samego punktu).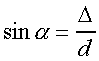
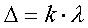
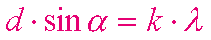
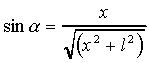
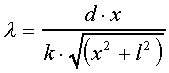

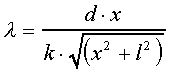
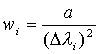
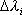 obliczamy jako błędy
maksymalne pomiarów pośrednich metodą różniczki zupełnej:
obliczamy jako błędy
maksymalne pomiarów pośrednich metodą różniczki zupełnej: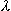 z funkcji
z funkcji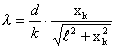

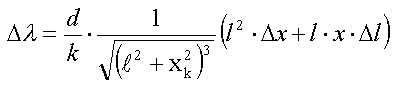
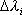 obliczamy średnią ważoną długość fali wg wzoru :
obliczamy średnią ważoną długość fali wg wzoru :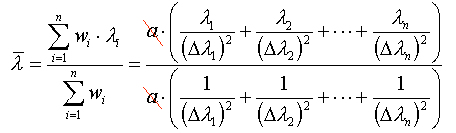
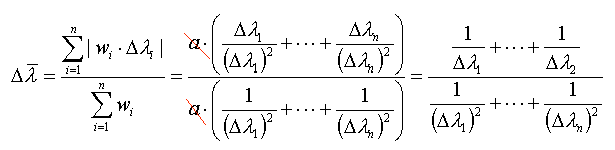
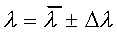
 Strony tytułowej
Strony tytułowej