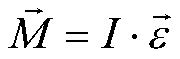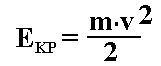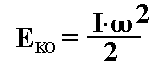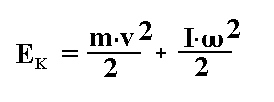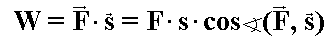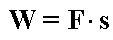Druga zasada dynamiki Newtona:
Jeżeli na ciało o pewnej masie m działają zewnętrzne siły
F1, F2, F3, F4 ..., to pod wpływem
tych sił ciało to porusza się z przyspieszeniem takim, że
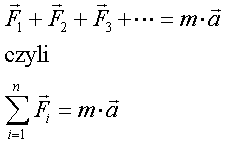
Bryła sztywna
to takie ciało, w którym pod wpływem dziłających
sił zewnętrznych nie zmienia się wzajemna odległość pomiędzy cząsteczkami tego
ciała (siły te nie zmieniają kształtu ciała). Z definicji wynika, że dane ciało
czasami możemy traktować jak bryłę sztywną (wtedy, gdy działające siły są zbyt małe aby to
ciało odkształcić), a innym razem, gdy działające siły są większe, ciało
przestaje być bryłą sztywną.
bryły sztywnej względem
pewnej osi (definiuje się również inne momenty bezwładności) nazywamy wyrażenie
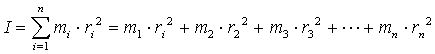 . Wzór ten odczytujemy następująco:
. Wzór ten odczytujemy następująco:
Aby znaleźć moment bezwładności ciała należy podzielić w myśli to ciało na
fragmenty tak małe, aby każdy można było traktować jak punkt materialny o pewnej
masie mi, pomnożyć jego masę przez kwadrat jej odlęgłości od
osi obrotu ri2 i wszystkie otrzymane iloczyny do
siebie dodać. Ta dosyć skomplikowana recepta może być zastoswana praktycznie
tylko do ciał, które składają się ze skończonej liczby niewielkich elementów,
które można potraktować w przybliżeniu jak zbiór niezależnych punktów
materialnych. W praktyce, do ciał rzeczywistych, a więc takich dla których masa
jest rozłożona w sposób ciągły stosuje się postać całkową definicji pozwalającą
obliczać rzeczywiste momenty bezwładności:
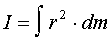
We wzorze tym r2 oznacza zmienną określającą odległość
elementu masy dm od osi obrotu.
W oparciu o tę zależność można stosunkowo prosto wyliczyć moment bezwładności
kilku popularnych brył:
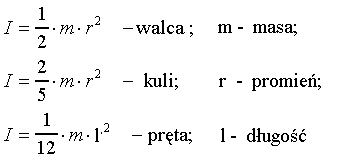
Wszystkie powyższe wzory określają moment bezwładności
brył względem osi przechodzących przez środek masy danej bryły.
Do określenia momentu bezwładności względem innej osi pomocne jest
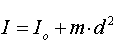
 Twierdzenie to mówi, że jeśli znamy moment bezwładności
Io danego ciała względem pewnej osi przechodzącej przez środek
masy tego ciała,
Twierdzenie to mówi, że jeśli znamy moment bezwładności
Io danego ciała względem pewnej osi przechodzącej przez środek
masy tego ciała,
to aby obliczyć moment bezwładności I
względem dowolnej innej osi równoległej do niej,
należy do momentu
Io dodać iloczyn masy ciała i kwadratu odległości d
między tymi osiami czyli md2:
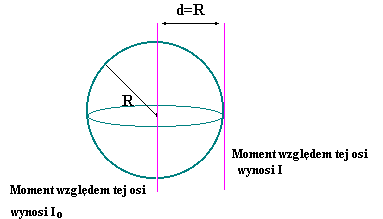
Ilustruje to rysunek powyżej, na przykładzie którego możemy wyliczyć moment
bezwładności kuli względem osi stycznej do kuli:
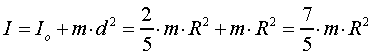
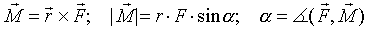
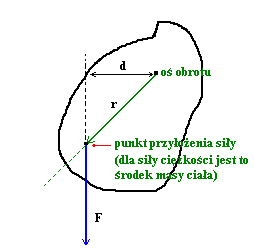
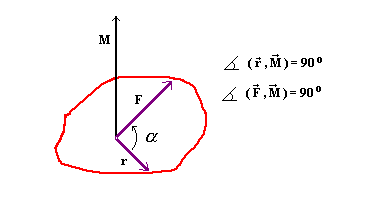
Moment M siły działającej na ciało to wielkość wektorowa określona przez
iloczyn wektorowy działającej siły i promienia.
Wektor momentu siły jest prostopadły do płaszczyzny wyznaczonej przez wektor
siły i wektor r, a jego zwrot określa reguła śruby prawoskrętnej.
Zgodnie z tą regułą, jeśli będziemy obracali po najkrótszej drodze
pierwszy wektor (tu: r) tak, aby pokrył się z drugim (tu: F),
to obracana w tym samym kierunku śruba prawoskrętna będzie przesuwać się
(będzie wkręcana lub wykręcana) w kierunku określającym zwrot wektora M
obracającej się bryły to
charakterystyczna dla ruchu obrotowego wielkość określająca kąt zakreślany przez
bryłę w określonym czasie. 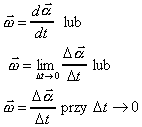
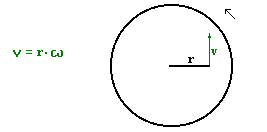
Każdy punkt obracającej się bryły ma inną prędkość liniową, natomiast prędkość
kątowa wszystkich punktów bryły jest taka sama. Punkt odległy od osi obrotu
o r ma prędkość liniową v taką, że
 Należy pamiętać, że wektor prędkości kątowej jest prostopadły do płaszczyzny
ruchu.
Należy pamiętać, że wektor prędkości kątowej jest prostopadły do płaszczyzny
ruchu.
obracającej się bryły
określamy jako zmianę prędkości kątowej tej bryły w czasie.
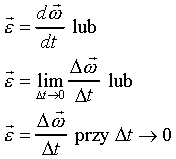
Każdy punkt obracającej się bryły ma inne przyspieszenie liniowe, natomiast
przyspieszenie kątowe wszystkich punktów bryły jest takie samo.
Punkt odległy od osi obrotu o r ma przyspieszenie liniowe a
takie, że
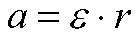 Należy pamiętać, że wektor przyspieszenia kątowego jest prostopadły do płaszczyzny
ruchu.
Należy pamiętać, że wektor przyspieszenia kątowego jest prostopadły do płaszczyzny
ruchu.
Mówi ona, że jeśli na pewne ciało, które posiada pewien swój
moment bezwładności I zadziałają zewnętrzne siły, które wywrą na to ciało
pewien wypadkowy moment siły M, to w wyniku tego działania ciało będzie obracać
się z przyspieszeniem kątowym  takim, że
takim, że
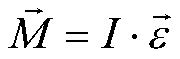 bryły sztywnej jest sumą
energii kinetycznej jej ruchu postępowego Ekp i energii kinetycznej
jej ruchu obrotowego Eko.
bryły sztywnej jest sumą
energii kinetycznej jej ruchu postępowego Ekp i energii kinetycznej
jej ruchu obrotowego Eko.
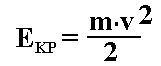
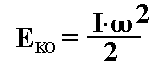
Prędkość v występująca we wzorze określa prędkość środka masy bryły, tak
więc dla bryły, która nie przemieszcza się (n.p. tzw. blok nieruchomy),
występuje tylko energia Eko związana z obrotem ciała.
Natomiast dla np. toczącej się kuli oba te składniki mają znaczenie i wtedy
całkowita energia kinetyczna Ek wynosi:
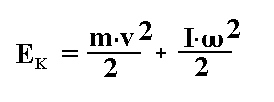
nazywamy iloczyn skalarny siły F
działającej na ciało i wektora przemieszczenia s jaki ta siła
wywołała:
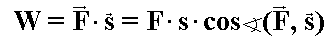
Gdy działająca siła jest zgodna z kierunkiem przemieszczenia, cosinus we wzorze
=1 i wzór można zapisać po prostu jako
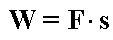
.
Gdy siła działa prostopadle do kierunku przemieszczenia, jej praca wynosi 0.
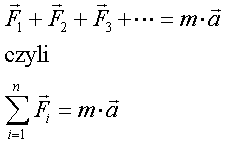
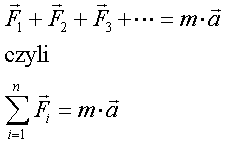
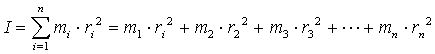
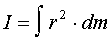
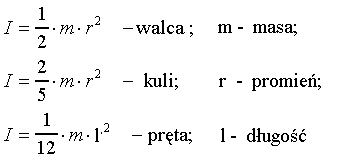
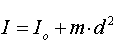
 Twierdzenie to mówi, że jeśli znamy moment bezwładności
Io danego ciała względem pewnej osi przechodzącej przez środek
masy tego ciała,
Twierdzenie to mówi, że jeśli znamy moment bezwładności
Io danego ciała względem pewnej osi przechodzącej przez środek
masy tego ciała,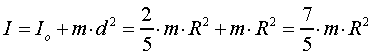
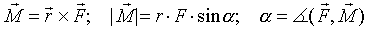
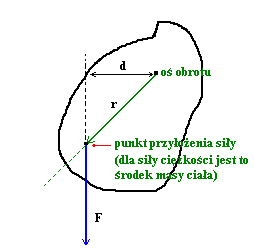

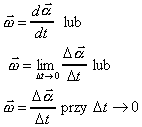

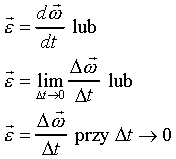
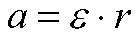
 takim, że
takim, że