Prąd wypływający ze źródła prądu stałego U, rozgałęzia się zgodnie z
I prawem Kirchhoffa
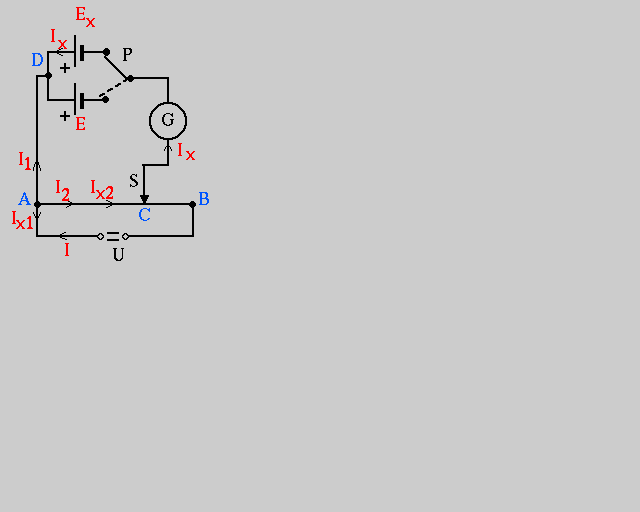
na prądy:I2 - płynący przez strunę A-B z powrotem do źródła U oraz
I1 - płynący przez (włączone w danej chwili) źródło Ex, przełącznik P, galwanometr G i dalej, przez odcinek C-B struny, z powrotem do źródła U.
Z badanego źródła (np Ex) wypływa drugi prąd oznaczony na rysunku jako Ix, płynący przez punkt D, rozgałęziający się w punkcie A na prądy Ix2 oraz Ix1.
(Prąd Ix2 płynie przez strunę, a prąd Ix1 przez źródło U).
Od punktu C oba te prądy, znow jako Ix, przez galwanometr G i przełącznik P wracają do badanego źródła. Przesuwając suwakiem S wzdłuż struny można znaleźć taki punkt C (taką oporność odcinka A-C), by natężenie prądu I x było dokładnie równe I1 (pod warunkiem, że U > Ex - dlaczego?). Wówczas wskazanie galwanometru będzie równe 0, a zatem sumaryczny prąd płynący przez źródło Exwynosi też 0. Mówimy, że prądy I1 i Ix kompensują się nawzajem. A ponieważ spełniony został warunek, aby przez badane źródło nie płynął prąd, napięcie panujące na źródłe badanym (a więc i na odcinku A-C struny), równe jest teraz jego SEM.Aby wyznaczyć tę wartość SEM skorzystamy z II prawa Kirchhoffa i wzoru na opór przewodnika o kształtach regularnych.
Ex= I . RAC = I . q . lx / S
gdzie:lx - długość odcinka AC
q - opór właściwy struny
S - pole przekroju poprzecznego struny
Jeżeli włączymy w obwód zamiast ogniwa badanego ogniwo wzorcowe o znanej SEM równej Eo i skompensujemy je ustawiajac suwak S w jakimś punkcie C' to uzyskamy równanie:
Eo= I . RAC' = I . q . lo / S
gdzie:lo - długość odcinka AC'
W obu przypadkach natężenie prądu I płynącego przez odcinek AC (lub AC') jest takie samo, gdyż w obu przypadkach natężenie prądu w części A-D-P-C (lub A-D-P-C') jest równe zeru.
Po podzieleniu stronami obu powyższych równań otrzymujemy wzór, przy pomocy którego wyliczymy szukaną SEM:
Ex=Eo . lx / lo
Jak widać wystarczą dwa pomiary długości lo i lx oraz znajomość Eo, aby wyznaczyć nieznaną SEM źródła.